An English version of this document is available.
Anmerkung: Das folgende Dokument benutzt die Windows-Schriftart Symbol zur Darstellung griechischer Buchstaben. Wenn ihr Browser die Darstellung dieser Zeichen nicht unterstützt, so sehen sie an ihrer Stelle die entsprechenden lateinischen Buchstaben (D=Delta, e=Epsilon, s=Sigma, p=Pi)
Ich freue mich jederzeit über Anregungen (zum Beispiel neue Anwendungsbeispiele)
dieses Programm betreffend. Ebenfalls dankbar bin ich für Hinweise
auf Fehler im Programm oder in diesem Dokument.
Feedback bitte an Matthias Benkmann (m.s.b (a) gmx.net)
Außerdem freut es mich natürlich, wenn dieses Programm weitergegeben
wird. Es ist kostenlose Software (Freeware), absolut kostenlos.
Dieses HTML-Dokument ist das offizielle Handbuch zum Molekular-Dynamik-Simulator (MDS). Es ist im Download des Programms außerdem noch als unformatierter ASCII-Abzug dieser Seite enthalten.
Wir alle haben eine intuitive Vorstellung von Begriffen wie "warm"
oder "kalt". Ebenso wissen wir, was wir uns unter einer Flüssigkeit
vorzustellen haben. Doch wenn man genauer nachfragt, was diese Begriffe
auf mikroskopischer Ebene bedeuten, werden viele Menschen keine Antwort
darauf wissen. Andererseits gibt es jedoch Phänomene, die man sich
sehr gut veranschaulichen kann, wie zum Beispiel die um die Sonne kreisenden
Planeten. Man muß nur einen Globus in die Mitte des Zimmers stellen
und mit einer Murmel in der Hand um ihn herumgehen. Die Kepler-Gesetze
wird man sich so freilich schwer vor Augen führen können.
Manchmal ist es mit schulischen Mitteln unmöglich, Experimente vorzuführen,
um dem Lernenden einen Sachverhalt näher zu bringen. Die Möglichkeiten
des Lehrers erschöpfen sich oft in statischen Bildern. Ein Beispiel
hierfür ist die modellhafte Erklärung der Aggregatszustände
anhand von dicht und weniger dicht gepackten Kugeln. Und auch wenn ein
Film zur Verfügung steht, so hat dieser doch das große Manko
der fehlenden Interaktivität.
Bei all diesen Problemen kann der Computer dem Lehrer hilfreich zur Seite stehen. Daher wird er mit Sicherheit eines der wichtigsten Mittel des zukünftigen Unterrichts sein. Computerprogramme können zwar das Realexperiment nicht ersetzen, bieten aber die Möglichkeit, Sachverhalte zu simulieren, die sich dem wirklichen Versuch ganz oder teilweise entziehen. Zudem ergibt sich die Möglichkeit, aktiv in das Bildschirmgeschehen einzugreifen und sogar Unmögliches, zum Beispiel umgekehrte Gravitation, auszuprobieren.
Kurzbeschreibung des Programms
Das Programm "Molekular-Dynamik-Simulator" (MDS) wurde entwickelt, um die Vorgänge in einem Vielteilchensystem zu simulieren. Selbstverständlich ist es auch möglich, und je nach Zusammenhang auch sinnvoll, sich auf einige wenige Teilchen zu beschränken. Bei der Gestaltung des Programms wurde darauf geachtet, ein ansprechendes und farbenfrohes Äußeres mit maximalem Bedienkomfort zu verbinden, ohne jedoch Abstriche bei der dahinterstehenden Physik zu machen.
Das Programm erfordert einen IBM-kompatiblen PC. Eine CPU des Typs i80386 (oder kompatibel) ist mindestens erforderlich, ebenso ein i80387 kompatibler Koprozessor. Eine 100% zum IBM Video Graphics Array (VGA) kompatible Grafikkarte mit Farbmonitor ist außerdem notwendig. Das Programm ist lauffähig unter DOS ab Version 3.0 und in Vollbild DOS-Sitzungen unter allen Betriebssystemen, die mindestens 502000 Byte freien konventionellen Speicher bieten und dem Programm direkte Zugriffe auf die Register der Grafikkarte sowie des PIT (Programmable Interval Timer) gestatten. Zu beachten ist dabei, daß je nach Betriebssystem und Grafikkartentreiber der vom Programm verwendete 360x480 "tweaked" Modus nach einer Taskumschaltung evtl. nicht wieder restauriert werden kann. Obwohl außerordentlich unwahrscheinlich und bis dato nicht beobachtet, ist eine Beschädigung durch falsche Synchronisation bei älteren Monitoren nicht auszuschließen. Daher sollte während der Arbeit mit dem Molekulardynamik-Simulator (MDS) nicht zwischen mehreren Applikationen umgeschaltet und vor Programmstart der Bildschirmschoner deaktiviert werden. Im Ernstfall sollte der Molekulardynamik-Simulator sofort mit der Tastenkombination ALT-X (evtl. zweimal, falls die Simulation gerade läuft) verlassen werden.
DER PROGRAMMIERER WEIST DARAUF HIN, DASS ES SICH BEI DIESEM PROBLEM UM EINEN FEHLER IN DER ENTSPRECHENDEN BETRIEBSSYSTEM-SOFTWARE UND NICHT IN MDS HANDELT. BEI BEACHTUNG DER OBEN GENANNTEN MASSNAHMEN ODER BENUTZUNG UNTER DOS SIND KEINE SCHÄDEN ZU BEFÜRCHTEN.
AUCH IM FALLE VON DURCH DEN PROGRAMMIERER VERSCHULDETEN FEHLERN ÜBERNIMMT
DIESER KEINERLEI HAFTUNG IRGENDEINER ART. DIES GILT INSBESONDERE FÜR,
IST ABER NICHT BESCHRÄNKT AUF DIREKTE ODER INDIREKTE SCHÄDEN
IN ZUSAMMENHANG MIT DIESER SOFTWARE. DER BENUTZER MUSS VOR JEDEM AUSFÜHREN
DER SOFTWARE SICHERSTELLEN, DASS DIESE REGELUNG IN DEM GEBIET, UNTER DESSEN
GERICHTSBARKEIT ER FÄLLT, LEGAL IST. IST DIES NICHT ODER NUR TEILWEISE
DER FALL, SO UNTERSAGT DER PROGRAMMIERER JEDWEDES AUSFÜHREN DER SOFTWARE.
(BEACHTEN SIE DIE VOLLSTÄNDIGEN BENUTZUNGSBESTIMMUNGEN IN DER DATEI
LIESMICH.TXT BEVOR SIE DAS PROGRAMM AUSFÜHREN.)
Das Programm testet zu Beginn, ob das System die Mindestvoraussetzungen erfüllt und bricht mit einer Fehlermeldung ab, falls dies nicht der Fall ist. Es ist jedoch möglich, daß Ihre VGA-Karte nicht 100% IBM kompatibel ist, und das Programm trotzdem startet. In diesem Fall wird die Bildschirmausgabe verstümmelt sein. Sie können das Programm jedoch mit der Tastenkombination ALT-X verlassen.
Die Bewegung der Teilchen wird schrittweise simuliert. In jedem Schritt werden die, durch die Wechselwirkungspotentiale hervorgerufenen Kräfte auf die Teilchen berechnet und summiert. Aus diesen Kräften wird dann mit den Gleichungen F=ma, v=v0+a*Dt, x=x0+v*Dt der neue Ort und die neue Geschwindigkeit für jedes Teilchen berechnet. Der zugrunde gelegte Zeitschritt Dt ist vom Benutzer einstellbar.
Den Werten im Programm sind die entsprechenden SI-Einheiten zugrunde
gelegt.
Die Winkel zwischen den Geschwindigkeitskomponenten, werden in Grad angegeben,
was im Eigenschaften-Menü noch gesondert
mit [°] gekennzeichnet ist.
In den Anzeigen bedeuten +INF und -INF
(INFinite=unendlich), daß bei dem gewählten Aufbau entweder
der entsprechende Wert außerhalb des Anzeigebereichs liegt, oder
daß eine Division durch Null stattgefunden hat. Letzteres tritt für
gewöhnlich auf, wenn der Benutzer aus Versehen zwei Teilchen auf exakt
die selbe Raumposition setzt und damit ihr Abstand 0 beträgt, so daß bei der
Berechnung des Potentials durch 0 dividiert wird.
+NAN und -NAN (Not A Number= keine Zahl) treten für
gewöhnlich auf, wenn (ebenfalls aufgrund eines fehlerhaften Aufbaus)
in einer Formel eine Rechenoperation auftritt, die nicht definiert und
außerdem nicht mit einer Unendlichkeit zu beantworten ist (z.B. Wurzel
einer negativen Zahl).
Das Programm ist jedoch so gutmütig, daß es sowohl das auftreten
einer Unendlichkeit, als auch einer NAN, nicht mit einer Fehlermeldung
oder gar einem Absturz bestraft. Es steht deshalb dem hemmungslosen Herumspielen
mit den Einstellungen nichts im Wege.
Unterstützte Wechselwirkungspotentiale
Für die Wechselwirkungen zwischen den Teilchen stehen zur Simulation im Molekular-Dynamik-Simulator die unten in der Tabelle aufgeführten Potentiale zur Verfügung. Des weiteren besteht die Möglichkeit, die Teilchen über harte Stöße wechselwirken zu lassen.
| Potential | Epot ij | Fij | Epot=0 bei | F=0 bei | Anwendungsbeispiel |
| Lennard Jones | -4es6(r6-s6)/r12 | 24es6(r6-2s6)/r13 | |r|=s | |r|=s*21/6 | van-der-Waals-KrÄfte bei Edelgasen |
| Quadratisch | -e+36e*(r-r0)2/r02 | 72e*(r-r0)/r02 | r=7r0/6 oder r=5r0/6 | r=r0 | Pseudo-Gas(Atome mit Hookschen Federn verbunden) Näherung für Lennard Jones |
| Gravitation | -G*mi*mj/r | G*mi*mj/r2 | _____ | ______ | Kepler-Gesetze |
| Coulomb | qi*qj/(4pe0r) | -qi*qj/(4pe0r2) | _____ | ______ | Bohrsches Atommodell |
Epot ij ist die potentielle Energie
des Teilchenpaares ij. Negative Werte bedeuten, daß sich die Teilchen
gegenseitig anziehen.
Fij ist die Kraft, die die Teilchen i und
j aufeinander ausüben. Positive Werte bedeuten Anziehung.
r0 ist der Abstand zwischen zwei Teilchen
bei dem gilt Fij=0.
e,s sind von der Teilchenart abhängige
Konstanten.
G ist die Gravitationskonstante.
qi,qj ist
die Ladung des Teilchens i bzw. j .
e0 ist die elektrische
Feldkonstante

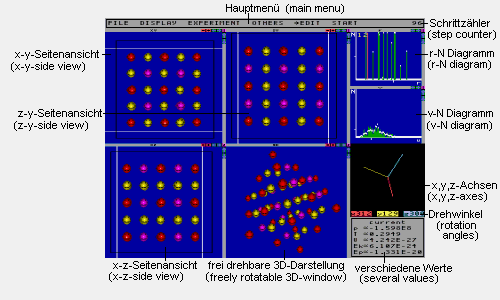
Dieses Bild zeigt alle Fenster des Programmes. Alle, bis auf das Hauptmenü, lassen sich unabhängig voneinander ein- und ausschalten.
Hauptmenü: Hier befinden sich die
Untermenüs "File","Display","Experiment"
und "Others", sowie der Knopf zum Umschalten
zwischen View-Modus und Edit-Modus und der Knopf
zum Starten/Anhalten der Simulation. Links-Click öffnet die Menüs
bzw. aktiviert die Knöpfe.
Schrittzähler: Zählt die
bis jetzt errechneten Schritte des momentan laufenden Experiments
r-N-Diagramm: Zu jedem Abstand r ist
hier die Anzahl Nachbarteilchen eingetragen, die man in diesem Abstand
von einem Teilchen durchschnittlich findet. Die momentanen Werte sind durch
grüne Striche, die gemittelten Werte durch weiße Punkte dargestellt.
Die Einheit der horizontalen Achse ist 360/scale
Meter abgerundet auf die nächste 10er-Potenz (scale
ist der im Menü Display/Diagrams bei
scale angegebene Wert.). Die Einheit
der vertikalen Achse ist 1.
Die erste gelbe Zahl gibt die durchschnittliche Anzahl nächster
Nachbarn (Teilchen deren Abstand kleiner ist, als der unter Display/Diagrams/next
sum r angegebene Wert) eines Teilchens an. Die zweite gelbe Zahl
zeigt die durchschnittliche Entfernung eines nächsten Nachbarn an.
Die rote Linie befindet sich bei der Entfernung Display/Diagrams/next
sum r.
v-N-Diagramm: Zu jeder Geschwindigkeit
v ist die Anzahl Teilchen mit dieser Geschwindigkeit eingetragen. Die
Werte der aktuellen Simulation sind durch grüne Striche,
die gemittelten Werte durch weiße
Punkte dargestellt.
Die Einheit der horizontalen Achse ist 360/scale
Meter pro Sekunde abgerundet auf die nächste 10er-Potenz (scale
ist der im Menü Display/Diagrams bei
scale angegebene Wert.). Die Einheit
der vertikalen Achse ist 1.
verschiedene Werte: Dieses Fenster
zeigt die Werte für Druck (p), Temperatur (T), Volumen(V) und die
durchschnittliche kinetische Energie pro Teilchen (Ek) , sowie die durchschnittliche
potentielle Energie pro Teilchen (Ep) an. Über den current/mean
Knopf läßt sich die Anzeige zwischen Momentan- und Mittelwerten
umschalten. Für Ek und T lassen sich neue Werte eingeben, die sofort
aktiv werden. Für das Volumen läßt
sich ein Zielvolumen eingeben, das während der Simulation durch verschieben
der Wände in Schritten zu je ½Ds
angesteuert wird (½Ds
läßt sich über Experiment/Parameters/
½Ds einstellen).
Achtung: Die Eingabe eines Zielvolumens deaktiviert die Druckanpassung.
frei drehbare 3D-Darstellung: Dieses
Fenster zeigt das Teilchenensemble um die x-,y- und z-Achse gedreht in
Zentralperspektive. Die Drehreihenfolge ist z-Drehung, x-Drehung, y-Drehung.
Bei Links-Click auf ein Teilchen in diesem Fenster öffnet sich das
Eigenschaften-Menü, in dem die Eigenschaften
des angeclickten Teilchens dargestellt sind und verändert werden können..
x,y,z-Achsen: Dieses Fenster zeigt die
x-,y- und z-Achse den momentanen Drehwinkeln entsprechend rotiert (Parallelprojektion).
Bei Links-Click in dieses Fenster des Molekulardynamik-Simulator können
bei gedrückt gehaltener
Maustaste die Achsen gedreht werden. An der Unterkante des Fensters sind
die Drehwinkel angegeben. Bei Links-Click
auf eine der Ziffern wird diese mit Übertrag um eins erhöht,
bei Rechts-Click um eins erniedrigt. Wird die Maustaste gedrückt gehalten,
so wird nach einer kleinen Verzögerung kontinuierlich gedreht.
Seitenansicht-Fenster: Diese
Fenster zeigen die entsprechenden Seiten des Ensembles (Parallelprojektion).
Die schwarzen Rechtecke stellen die Begrenzungslinien
des Volumens, in dem die Teilchen gefangen sind, dar. Ihre Anzeige kann
mit Display/Smiley Windows/draw borders
ein- bzw. ausgeschaltet werden.
Die weißen Linien, die mit der Maus bei
gedrückter linker Taste verschoben werden können, bestimmen die
momentanen Sichtebenen. Nur Teilchen, die sich zwischen den weißen
Linien befinden, werden dargestellt. Alle anderen Teilchen sind (auch im
3D-Fenster) unsichtbar. Man kann die Sichtebenen
mit Display/Smiley windows/Reset view levels
auf einmal auf die maximalen Grenzen zurücksetzen.
Ein Links-Click auf ein Teilchen in den Seitenansicht-Fenstern
oder im 3D-Fenster öffnet das Fenster mit den Teilcheneigenschaften.
In der frei drehbaren 3D-Darstellung und in den Seitenansicht-Fenstern
kann mit den Pfeiltasten der Fensterinhalt verschoben werden. Die Knöpfe
+ und - an der Oberkante der Fenster ermöglichen es, den dargestellten
Ausschnitt näher heran oder weiter weg zu zoomen. Die Pfeile an den
Rändern der Teilchen- und Diagramm-Fenster
ermöglichen es, die Fenstergrößen anzupassen, indem man
sie mit der linken Maustaste anclickt und bei gedrückter Taste die
Maus zieht.
Der mit "Z" markierte Knopf in der oberen
rechten Ecke der Fenster zoomt das entsprechende Fenster auf maximale Größe.
Ein weiterer Click stellt den Ausgangszustand wieder her.
Wird mit der rechten Maustaste in ein Fenster geclickt, und die Maus bei
gedrückter Taste in ein anderes Fenster gezogen wird, so werden die
beiden Fenster vertauscht.
MAIN MENU
-->edit/view schaltet in den angegebenen
Modus. (siehe "Der Edit-Modus")
start startet die Simulation, sofern der Schrittzähler
nicht Experiment/Parameters/Max. steps
bereits erreicht hat.
FILE
Load öffnet das Dateiauswahlfenster zum Laden
einer .MDS Datei.
Save öffnet das Dateiauswahlfenster zum
Speichern einer .MDS Datei.
Grab PCX öffnet das Dateiauswahlfenster
zum Speichern eines Screenshots als .PCX Datei.
Quit beendet das Programm.
DISPLAY
invisibles schaltet die Anzeige als unsichtbar
markierter Teilchen ein bzw. aus.
slicing siehe Display/Smiley Windows/Slicing.
D-Scheme ändert die Anordnung der Fenster.
Step counter schaltet die Anzeige des
Schrittzählers ein bzw. aus.
DIAGRAMS
r-distribution schaltet die Anzeige des
r-N-Diagrammes ein bzw. aus.
after steps gibt an, nach wievielen
Schritten das Diagramm neu berechnet wird und die Werte zu den Mittelwerten
addiert werden.
scale ist ein Faktor zur Umrechnung
der Fließkommawerte in ganze Zahlen vor Eintragung ins Diagramm.
Scale ist indirekt proportional zur Einheit der
horizontalen Achse.
offset gibt an, um wieviel das Diagramm nach
links geschoben werden soll.
devalue after gibt an, nach wievielen
Diagrammaktualisierungen der Inhalt des Puffers für die Diagrammittelwerte
halbiert werden soll. Diese Funktion sorgt dafür, daß auch nach
einer großen Anzahl von Schritten die Diagrammittelwerte noch auf
Veränderungen reagieren. Wird hier 0 angegeben ist die Funktion deaktiviert.
next sum r gibt an, bis zu welcher Entfernung
ein Teilchen als nächster Nachbar
gezählt wird.
v-distribution schaltet die Anzeige
des v-N-Diagrammes ein bzw. aus.
Reset mean values startet
die Mittelwertberechnung der Diagramme neu.
MISCELLANEOUS
Miscellaneous schaltet die Anzeige der Werte für p,V,T,Ek
und Ep ein bzw. aus.
after steps gibt an, nach wievielen
Schritten die Werte neu berechnet werden.
mean buf size gibt an, über wieviele
der nach after steps Schritten erfolgten
Berechnungen der Werte gemittelt werden soll. Wird hier 0 angegeben, so
erfolgt die Mittelung über alle seit dem letzten Reset der Mittelwerte
berechneten Werte.
Reset mean values startet die
Mittelwertberechnung neu.
SMILEY WINDOWS
Rotatable 3D schaltet die Anzeige des frei
drehbaren 3D-Fensters ein bzw. aus.
x,y,z axes schaltet die Anzeige des x,y,z-Achsen-Fensters
ein bzw. aus.
slice start bestimmt, wie weit, die im
3D-Fenster dargestellte Schicht vom Betrachter
weg ist (gemessen in Pixeln).
thickness bestimmt, wie dick die im 3D-Fenster
dargestellte Schicht ist (gemessen in Pixeln).
slicing sorgt dafür, daß
im 3D-Fenster nur Teilchen dargestellt werden,
die in der durch slice start und
thickness bestimmten Schicht liegen. Dies
ist sehr nützlich, wenn zum Beispiel bei einem FCC-Gitter
die hexagonale Grundstruktur betrachtet werden soll. Man definiert hierfür
eine Schicht mit slice start und
thickness und dreht dann die 3D-Darstellung,
bis die Struktur zu erkennnen ist.
x-y side view, x-z side view, z-y side view
schaltet die Anzeige des entsprechenden
Fensters ein bzw. aus.
after steps gibt an, nach wievielen
Schritten das 3D-Fenster und die Seitenansichten
aktualisiert werden.
slime tracks läßt die Teilchen
eine Spur hinter sich herziehen.
draw borders schaltet die Anzeige der
Volumengrenzen ein bzw. aus.
smiley size bestimmt die Größe
der Teilchen in den Fenstern, falls r-scaling
deaktiviert.
z-scaling schaltet die Skalierung der Teilchengröße
in Abhängigkeit von der Entfernung zum Betrachter auch für die
Seitenansichten ein (in der 3D-Darstellung
wird immer z-skaliert).
r-scaling schaltet die Skalierung der Teilchengröße
in Abhängigkeit vom Radius ein bzw. aus.
Reset view levels setzt die Sichtebenenbegrenzungen
auf die Maximalwerte.
v-vectors schaltet die Anzeige der Geschwindigkeitsvektoren
ein bzw. aus.
scale bestimmt den Faktor mit dem
die Längen der Geschwindigkeitsvektoren vor ihrer Einzeichnung multipliziert
werden.
EXPERIMENT
Description zeigt die Beschreibung des momentanen
Experiments an und ermöglicht ihre Veränderung.
Reset step counter setzt den Schrittzähler
auf 0 und definiert damit den Beginn eines neuen Experiments, d.h. Restart experiment
stellt jetzt den zum Zeitpunkt des Reset bestehenden Aufbau wieder her.
Restart experiment stellt den Startaufbau
des momentanen Experiments wieder her. Ein neues Experiment beginnt bei
einem Reset step counter, load
(mit properties aktiviert) oder Experiment/Build lattice/build lattice.
POTENTIAL TYPE
Lennard Jones, Quadratic, Gravity, Coulomb wählt das entsprechende
Potential für die Molekular-Dynamik-Simulation aus. Mehrere Potentiale können gleichzeitig
aktiviert sein.
s,e,e0,r0,G
sind die potentialspezifischen Konstanten. Näheres zu den Potentialen
siehe oben bei "Unterstützte
Wechselwirkungspotentiale".
cutoff gibt den Abstand zweier Teilchen an,
ab dem die Wechselwirkungen des entsprechenden Potentials ignoriert werden.
Ein Cutoff kann benutzt werden, um Rechenzeit zu sparen. Achtung: Wenn
das quadratische Potential als
Näherung für das Lennard
Jones Potential benutzt werden soll, muß Cutoff<=7r0/6
gelten.
PARAMETERS
Dt bestimmt den
der Simulation zugrunde liegenden Zeitschritt.
collision check schaltet harte Stöße
bei Berührung zweier Teilchen ein bzw. aus. Achtung: Kollisionen werden
mit dem Teilchenradius berechnet, der im Eigenschaften-Menü
eingestellt ist, nicht mit dem Radius in den Darstellungen.
downwards gravity schaltet für
alle Teilchen konstante Beschleunigung in negative y-Richtung ein bzw.
aus.
g ist die Beschleunigung für downwards
gravity.
p schaltet Volumenanpassung zum Druckausgleich ein
bzw. aus.
Achtung: Wird Druckausgleich aktiviert, wird ein zuvor im Verschiedene-Werte-Fenster
eingegebenes Zielvolumen unwirksam. Ebenso deaktiviert die Eingabe eines
Zielvolumens die Druckanpassung.
target gibt den Zieldruck an, den
die Volumenanpassung zu erreichen sucht.
V-adapt Dsteps
gibt an, in welchem zeitlichen Abstand die Volumenanpassungen
durchgeführt werden sollen.
½ Ds
gibt an, um wieviel jede der 6 Wände bei der Volumenanpassung
verschoben wird.
c ist die Temperatur, die die Temperaturanpassung
in den nächsten Schritten zu erreichen versucht.
f gibt, falls exponentielle Erwärmung/Abkühlung
gewählt ist, den Faktor an, mit dem c nach
jeder Temperaturanpassung multipliziert
wird.
DT ist bei linearer
Erwärmung/Kühlung der Wert, der nach jeder Temperaturanpassung
zu c hinzugezählt wird.
Dsteps gibt
an, in welchem zeitlichen Abstand die Temperaturanpassungen
vorgenommen werden.
Max. steps gibt an, nach wievielen Schritten
die Simulation beendet werden soll. Achtung: Hat der Schrittzähler
diesen Wert einmal erreicht, so läßt sich die Simulation erst
wieder starten, wenn entweder der Schrittzähler auf 0 gesetzt wird
(Experiment/Reset step counter oder Experiment/Restart
experiment), oder Max. steps erhöht wird.
TEMPERATURE ADAPTION FUNCTIONS
free schaltet die Temperaturanpassung aus.
T=c, c=const. stellt die Temperaturanpassung
so ein, daß sie versucht, T konstant auf c zu halten.
T=c, c=c+ DT
stellt die Temperaturanpassung so ein, daß sie den angestrebten Wert
c in Schritten zu DT
verändert. Dies entspricht einer linearen Erwärmung/Abkühlung.
T=c, c=c*f stellt die
Temperaturanpassung so ein, daß sie den angestrebten Wert c
nach jeder Anpassung mit dem Faktor f multipliziert.
Dies entspricht einer exponentiellen Erwärmung/Abkühlung.
BOUNDARIES
Im blauen Fenster wird der virtuelle Kasten, in dem sich die Teilchen befinden
von vorne und von der rechten Seite durch schwarze Rechtecke dargestellt.
Die grünen Rechtecke geben das momentan von Teilchen ausgefüllte
Volumen wieder. Mit gedrückter linker Maustaste läßt sich
das Ensemble innerhalb des Kastens verschieben. Werden dabei Teilchen nach
außerhalb des Kastens verschoben, so erscheint an der entsprechenden
Seite ein roter Strich, um zu warnen, daß bei Bestätigung der
Verschiebung mit Set new boundaries
Teilchen gelöscht werden.
Achtung: Aufgrund einer geringen Toleranz ist es möglich, daß
trotz der Anzeige des roten Striches keine Teilchen gelöscht werden.
Periodic boundary schaltet die Rechnung
mit periodischen Randbedingungen ein
bzw. aus. Änderungen hier wirken sich bei Start der Simulation sofort
aus, ohne daß zuerst Set new boundaries
gewählt werden muß.
x,y,z gibt die momentane Länge der
entsprechenden Seite des Kastens an. Änderungen hier werden zwar sofort
im blauen Fenster dargestellt, werden aber erst nach Click auf Set
new boundaries aktiv. Vorher werden auch noch keine Teilchen außerhalb
des Kastens entfernt.
Set new boundaries setzt die veränderten
Seitenlängen und die im blauen Fenster ausgeführten Verschiebungen.
Teilchen außerhalb des Kastens werden gelöscht.
Die Teilchenzahl ist im Molekular-Dynamik-Simulationsprogramm im Vergleich
zur Realität sehr gering.
Wenn man einen Festkörper mit dem Molekulardynamik-Simulator (MDS) simuliert, ist daher der Anteil
von Randteilchen am Gesamtkörper sehr hoch. Dies sind Teilchen, die
weniger nächste Nachbarn als jene im
Inneren des Körpers haben. Darum werden sie weniger stark an ihrem
Platz gehalten, was dazu führen kann, daß sie sich vom Körper
lösen. Außerdem ergibt sich nicht die, für jeden Gittertyp
charakteristische Anzahl nächster Nachbarn. Mit Hilfe des "Rechentricks"
periodische Randbedingungen kann man diese Probleme beseitigen. Dabei 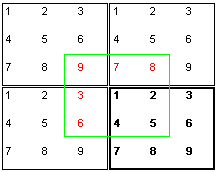 wird
bei der Berechnung so getan, als wären an den eigentlich berechneten
Kasten(stark umrandet) noch weitere identische Kästen angeschlossen.
Für die Berechnung der Kräfte, die auf ein Teilchen 1
wirken, werden dann die Nachbarteilchen aus einem virtuellen Kasten (grün
umrandet) herangezogen, in dessen Mitte Teilchen 1 steht.
So "sieht" das Teilchen 1 aus dem Beispiel nur die Teilchen
2,4 und 5 an ihrem wirklichen Ort. Die Teilchen 3,6,7,8
und 9 erscheinen ihm als virtuelle Teilchen 3,6,7,8
und 9. Man erkennt sofort, daß ein nahtloser
Übergang zwischen den Kästen nur gegeben ist, falls das Volumen
und die Teilchenaufstellung, wie hier im Bild, korrekt gewählt wird.
Wenn Experiment/Boundaries/periodic boundary
aktiv ist, achtet Experiment/Build lattice/build
lattice beim Aufbau auf eine nahtlose Fortsetzung des entsprechenden
Gittertyps. Falls sich jedoch im Verlaufe der Simulation der Gittertyp
ändert, muß manuell dafür gesorgt werden, daß das
Volumen für eine periodische Fortsetzung des entsprechenden Gittertyps
paßt (z.B. Im verschiedene-Werte-Fenster
ein Zielvolumen angeben).
wird
bei der Berechnung so getan, als wären an den eigentlich berechneten
Kasten(stark umrandet) noch weitere identische Kästen angeschlossen.
Für die Berechnung der Kräfte, die auf ein Teilchen 1
wirken, werden dann die Nachbarteilchen aus einem virtuellen Kasten (grün
umrandet) herangezogen, in dessen Mitte Teilchen 1 steht.
So "sieht" das Teilchen 1 aus dem Beispiel nur die Teilchen
2,4 und 5 an ihrem wirklichen Ort. Die Teilchen 3,6,7,8
und 9 erscheinen ihm als virtuelle Teilchen 3,6,7,8
und 9. Man erkennt sofort, daß ein nahtloser
Übergang zwischen den Kästen nur gegeben ist, falls das Volumen
und die Teilchenaufstellung, wie hier im Bild, korrekt gewählt wird.
Wenn Experiment/Boundaries/periodic boundary
aktiv ist, achtet Experiment/Build lattice/build
lattice beim Aufbau auf eine nahtlose Fortsetzung des entsprechenden
Gittertyps. Falls sich jedoch im Verlaufe der Simulation der Gittertyp
ändert, muß manuell dafür gesorgt werden, daß das
Volumen für eine periodische Fortsetzung des entsprechenden Gittertyps
paßt (z.B. Im verschiedene-Werte-Fenster
ein Zielvolumen angeben).
Neben oben genanntem Rechentrick bewirkt das Rechnen mit periodischen Randbedingungen
auch, daß Teilchen, die eine Seite des Kastens erreichen, nicht reflektiert,
sondern auf der anderen Seite wieder in den Kasten hineingesetzt werden.
BUILD LATTICE
x,y,z-direction cell no. gibt die Länge
der entsprechenden Seite, des zu erzeugenden Gitters, in Elementarzellen
an.
Unit cell side gibt die Seitenlänge
einer kubischen Elementarzelle an.
Velocity/p. gibt die beim Aufbau jedem
Teilchen zugeordnete Geschwindigkeit an. Die Geschwindigkeitsrichtungen
werden so verteilt, daß der Gesamtimpuls 0 ist. Ein Drehimpuls kann
jedoch vorhanden sein. Ist die sich ergebende Teilchenzahl ungerade, erhält
ein Teilchen die Geschwindigkeit 0.
Lattice type gibt die Art des aufzubauenden
Gitters an. Zur Auswahl stehen einfach kubisch (simple cubic), kubisch
flächenzentriert (face-centered cubic) und kubisch
raumzentriert (body-centered cubic).
Lattice error gibt an, ob das Teilchen
Nr. 0 eine 1prozentige Abweichung von der richtigen Startposition erhält,
um unrealistische Symmetrieerscheinungen zu vermeiden.
Build lattice baut das Gitter auf und
definiert damit den Beginn eines neuen Experiments (siehe Experiment/Restart
experiment). Falls Experiment/Boundaries/periodic
boundary aktiviert ist, wird das Gitter so aufgebaut, daß
es an den Grenzen des Kastens nahtlos periodisch
fortgesetzt werden kann.
OTHERS
Watchdogs gibt an, ob die Wachhunde frei sind.
Wenn ja, werden Teilchen außerhalb des Kastens totgebissen und die
Meldung "Woof!" ausgegeben. Falls Teilchen die eingestellte Maximalgeschwindigkeit
überschreiten, wird dies mit "Arf!" kundgetan. In letzterem
Fall werden die Teilchen am Leben gelassen.
Achtung: Während ein Überschreiten der Maximalgeschwindigkeit
im Verlaufe eines Experiments durchaus passieren kann, ist ein Verlassen
des Kastens durch ein Teilchen unter normalen Umständen ausgeschlossen,
da Teilchen an der Wand reflektiert (Experiment/Boundaries/periodic
boundary deaktiviert) oder an der anderen Seite wieder hineingesetzt
(periodic boundary aktiviert) werden.
Wenn dennoch ein Teilchen den Kasten verläßt, deutet dies auf
einen Aufbau mit zu hohen Kräften oder Geschwindigkeiten bzw. einen
für die Kräfte/Geschwindigkeiten zu großen Zeitschritt
hin. (siehe auch Hinweis zu den Anzeigen)
vmax gibt die von den Wachhunden
maximal tolerierte Geschwindigkeit an.
Current Smileys spiegelt die Gesamtanzahl
der Teilchen des Ensembles wieder.
Recalculate diagrams/misc. berechnet die
Diagramminhalte und p,T,Ek,Ep
neu. Diese Funktion ist nützlich, wenn man den Aufbau verändert
hat, und anhand der potentiellen Energie feststellen will, ob man eine
Konstellation mit übermäßig großen
Kräften erzeugt hat.
DAS EIGENSCHAFTEN MENÜ
Das Eigenschaften-Menü wird bei Links-Click auf ein Teilchen geöffnet.
Die folgenden Eigenschaften des Teilchens werden angezeigt und können
geändert werden:
Farbe, Gruppenstatus, Unsichtbarkeitsstatus,
Masse(m), Ladung(q), Radius(r), x,y und z-Koordinate, Geschwindigkeitsbetrag(v),
Winkel zwischen x-Komponente(vx) und y-Komponente(vy) des Geschwindigkeitsvektors,
Winkel zwischen vx und vz, Winkel zwischen vz und vy.
Über den Gruppenstatus ist es möglich
eine Gruppe von Teilchen zu definieren. Dies ist sinnvoll, wenn man mehrere
Teilchen auf einen Schlag verändern will (siehe Beispiel).
Man kann so, über die Option !DELETE
GROUP!, alle Teilchen der Gruppe (d.h.alle mit grouped: yes)
auf einmal löschen, oder, über die Option Group....=Smiley....
allen Teilchen der Gruppe den Wert .... des momentan angezeigten
Teilchens zuordnen (siehe Beispiel).
Mit Invert group wird die Gruppenzuordnung
umgekehrt, d.h. alle Teilchen, die zur Gruppe gehörten, gehören
jetzt nicht mehr dazu, und alle die vorher nicht bei der Gruppe waren,
bilden jetzt die Gruppe (siehe Beispiel).
Ungroup all setzt jedes Teilchen auf grouped:
no. Zusammen mit Invert group läßt
sich so leicht das ganze Ensemble verändern (siehe Beispiel).
Beispiel: Alle Teilchen sollen auf die Masse 1kg
gesetzt werden. Man setzt zuerst, das momentan angezeigte Teilchen auf
die Masse 1 (wie bereits erwähnt erfolgen alle Eingaben und Anzeigen
in den entsprechenden SI-Einheiten). Dann click man auf Ungroup
all, so daß kein Teilchen mehr zur Gruppe gehört. Mit
Invert group wird nun die Gruppenzugehörigkeit
aller Teilchen umgekehrt, d.h. jetzt gehören alle Teilchen zur Gruppe.
Mit Group m=Smiley m wird nun
allen Teilchen auf einmal die Masse 1kg zugeordnet.
Group smileys on screen setzt
bei allen Teilchen, die momentan auf dem Bildschirm zu sehen sind, grouped:
yes. Dies ist zum Beispiel sinnvoll, wenn man sich mit Display/slicing
in der frei drehbaren 3D-Darstellung
eine Schicht eines Kristalls herausgesucht hat, und nun alle Teilchen dieser
Schicht mit der gleichen Farbe einfärben will, um sie besser verfolgen
zu können.
Achtung: Wenn nur die Teilchen, die in der frei
drehbaren 3D-Darstellung zu sehen sind auf grouped:
yes gesetzt werden sollen, müssen vorher entweder die Seitenansichten
geschlossen, oder die frei drehbare 3D-Darstellung
gezoomt werden, denn Group
smileys on screen betrifft ALLE momentan sichtbaren Teilchen, nicht
nur die eines bestimmten Fensters.
Group follows smiley gibt an, ob bei
Verschieben eines Teilchens der Gruppe (siehe "Der
Edit-Modus"), die ganze Gruppe mitverschoben werden soll.
Achtung: Nur bei Verschiebung mit der Maus wird die Gruppe mitverschoben.
Bei direkter Änderung der x,y oder z-Koordinate, wird nur das Teilchen
verschoben.
Copy smiley erzeugt eine weiteres Teilchen
an der selben Position, wie das momentan angezeigte, mit den selben Eigenschaften.
Diese Option wird benutzt, um dem Ensemble neue Teilchen hinzuzufügen.
Achtung: Da das Teilchen auf exakt der selben Position wie die Vorlage
erzeugt wird, muß es unbedingt vor Beginn der Simulation an einen
anderen Platz gesetzt werden, da sonst das abstandsabhängige Potential
zwischen Vorlage und Kopie unendlich groß
wird, und bei Starten der Simulation das ganze Ensemble ins Unendliche
verschwindet.
!DELETE SMILEY! tut genau das was
man erwartet.
Während es im View-Modus nur möglich ist, die Position eines
Teilchens über das Eigenschaften-Menü
zu verändern, kann man nach Umschalten in den
Edit-Modus in den Seitenansicht-Fenstern
ein Teilchen mit gedrückt gehaltener linker Maustaste verschieben.
Falls das Teilchen der Gruppe angehört,
und die Option Group follows smiley
angeschaltet ist, wird die Gruppe mit verschoben.
Im Edit-Modus ist es außerdem möglich, durch einen Rechts-Click
auf ein Teilchen, die zuletzt an irgendeinem Teilchen durchgeführte
Eigenschaftsveränderung auf das angeclickte
Teilchen zu übertragen. Es genüg so zum Beispiel, ein Teilchen
im Eigenschaften-Menü grün
zu färben, dann kann man durch einfachen Rechts-Click andere Teilchen
grün färben.
Achtung: Löschen zählt ebenfalls als Eigenschaftsveränderung,
so daß, nachdem ein Teilchen gelöscht wurde, ein Rechts-Click
das angeclickte Teilchen entfernt. Der Edit-Modus ermöglicht auch,
sehr einfach neue Teilchen zu plazieren. Man muß nicht jedes Teilchen
einzeln mit Copy Smiley erzeugen und dann
an den richtigen Platz ziehen. Nachdem man ein Teilchen mit Copy
Smiley verdoppelt hat, kann man in den Seitenansicht-Fenstern
mit der rechten Maustaste neue Teilchen setzen. Die dritte Koordinate wird
jeweils vom zuletzt kopierten Teilchen übernommen.
Achtung: Es empfielt sich, nach Ändern des Ensembles Experiment/Reset
step counter zu wählen, oder das neue Ensemble abzuspeichern.
Dann kann man mit Experiment/Restart experiment
bzw. File/Load den Aufbau wiederherstellen,
nachdem das Experiment abgelaufen ist. Ansonsten ist der geänderte
Aufbau verloren.
Achtung: Wenn bei den folgenden Beispielen bestimmte Schrittzahlen, Drehwinkel oder Slicing-Parameter angegeben sind, wird davon ausgegangen, daß das Experiment bis zur entsprechenden Schrittzahl ohne Unterbrechung durchgerechnet wird. Falls dies nicht getan wird, und im Beispiel die Volumen-, Temperatur- oder Druckanpassungsfunktion benutzt wird, kann es zu leicht unterschiedlichen Ergebnissen kommen. Die beobachteten Strukturen und Werte werden nur im Mittel übereinstimmen. Dies erklärt sich dadurch, daß sich Iterationen selbst einfacher Funktionen nach vielen Schritten hochgradig chaotisch verhalten. Es kann sich insbesondere die Lage gesuchter Strukturen bezüglich des Betrachters verändern. Außerdem kann der exakte Wert einer Größe zu einem bestimmten Zeitschritt oder die Zahl der Zeitschritte bis zum Eintreten eines bestimmten Ereignisses leicht variieren.
1) Startbeispiel: Ausschnitt aus einem kristallinen Festkörper
Zielsetzung: Ziel dieses Versuchs ist die Demonstration einer für quadratisches und Lennard Jones Potential charakteristischen Struktur.
Aufbau: Die Ausgangslage ist ein kubisch flächenzentriertes Gitter bestehend aus 108 Teilchen. Als Gitterkonstante wurde 5.378Å gewählt, so daß der Abstand nächster Nachbarn bei r0 bezüglich s=3.4Å liegt. Die Startgeschwindigkeit ist 13.685m/s, d.h. die Temperatur beträgt 0.3K. Das standarmäßig gewählte Potential ist Lennard Jones mit einem Cutoff von 1m (d.h. länger als die Kastendiagonale, also deaktiviert). Periodische Randbedingungen sind aktiviert.
Durchführung und Beobachtungen: Nach Start der Simulation
bleibt, wie zu erwarten war, die Konfiguration stabil. Das r-N-Diagramm
zeigt deutliche Strukturen einer Nah- und Fernordnung. Hier wird außerdem
als Anzahl der nächsten Nachbarn die
für ein fcc-Gitter charakteristische Zahl
12 angezeigt. Lediglich die Geschwindigkeitsverteilung
verändert sich hin zur Maxwell-Verteilung. Nun wird im Menü Experiment/Potential
type der Cutoff für das Lennard Jones
Potential auf 4Å gesetzt, d.h. für die Berechnung der Potentiale
werden nur noch nächste Nachbarn herangezogen.
Als durchschnittliche potentielle Energie
pro Teilchen ergibt sich -1*10-20J.
Dies entspricht 6*(-e),
da ein Teilchen potentielle Energie bezüglich aller 12 nächsten
Nachbarn besitzt, und das Minimum des Lennard Jones Potentiales (pro Paar)
bei (r0/-e)
liegt. Dabei muß man beachten, daß nur die Hälfte der
potentiellen Energie eines Paares dem Teilchen zugeordnet werden darf (daher
6 und nicht 12).
Jetzt wird im Menü Experiment/Potential
type das Lennard Jones Potential deaktiviert, und das quadratische
Potential eingeschaltet. Es zeigt sich, daß die Anordung auch für
dieses Potential stabil ist. Dies ist eine Bestätigung dafür,
daß das quadratische Potential bei der Betrachtung von Kristallstrukturen
als Näherung für das Lennard Jones Potential benutzt werden kann.
Bei der potentiellen Energie pro Teilchen ergibt sich der Wert, der beim
Lennard Jones Potential nach Änderung des Cutoff
auftrat, da das quadratische Potential standardmäßig mit Cutoff
arbeitet.
Anmerkungen: Gelegentlich kann beobachtet werden, daß Teilchen von einer auf die andere Seite wechseln. Dies sind Teilchen, die am Rande des Kastens liegen und aufgrund der periodischen Randbedingungen bei seinem Verlassen auf der anderen Seite erscheinen.
Zielsetzung: Die Datei "kingas.mds" enthält ein Beispiel zur kinetischen Gastheorie. Es benutzt den Molekulardynamik-Simulator (MDS), um den theoretischen Betrachtungen der Schule Gestalt zu verleihen und die für die kinetische Gastheorie typischen Spurbilder demonstrieren. Auch die Diffusion kann an diesem Modell gezeigt werden.
Aufbau: Das Modellgas besteht aus 64 Teilchen der Masse 6.636*10-26kg und einem Radius von 2.5Å. Druck und Geschwindigkeit wurden so gewählt, daß die Anordung sich im Normzustand bei 1013hPa Druck und 273.15K Temperatur befindet. Ein Teilchen ist gelb markiert. Alle Teilchen außer diesem sind als unsichtbar markiert. Das Ensemble wird in Parallelprojektion betrachtet. Die Teilchen werden nach ihrer Größe skaliert.
Durchführung und Beobachtungen: Wie man in den Diagrammen
sieht, hat sich in dem System, das ursprünglich ein einfach kubisches
3x3x3 Gitter war, in dem alle Teilchen die
gleiche Geschwindigkeit hatten, nicht nur eine Maxwell-Verteilung bei der
Geschwindigkeit, sondern auch beim Abstand eingestellt.
a) typisches Spurbild
Wenn man nun Display/Smiley windows/slime
tracks anschaltet, und Display/invisibles
auf hidden stellt, dann kann man am gelben Teilchen die charakteristische
Spur eines Gasteilchens erkennen, das nur über elastische
Stöße mit anderen Teilchen wechselwirkt.
b) Random Walk
Wenn man nun die Geschwindigkeit des gelben Teilchens auf 0 setzt und seine
Masse stark erhöht (z.B. *50) kann man
den "Random Walk" eines Rauchteilchens in einem Gas beobachten.
Der Realitätsnähe wegen kann auch noch der Radius erhöht
werden.
c) Diffusion
Jetzt wird die Simulation angehalten und Display/invisibles
wieder auf shown gesetzt. Außerdem sollte Display/Smiley windows/slime
tracks wieder deaktiviert werden. Dann wird durch
Verschieben einer der beiden weißen Linien
das Ensemble in zwei Hälften geteilt und ein Teilchen der sichtbaren
Hälfte angeclickt. Mit Ungroup all
muß nun die Gruppenzuordnung aufgelöst werden. Mit Group
smileys on screen werden nun die sichtbaren Teilchen zur neuen
Gruppe. Nun wird das Teilchen durch Click auf Color umgefärbt
und die Farbe mit Group col=Smiley col
auf die ganze Gruppe übertragen. Nach zurückverschieben der weißen
Linie hat man nun zwei verschiedenfarbige Hälften, dies entspricht
zwei verschiedenen Gasen. Nach Herabsetzen von Experiment/Parameters/Dt
auf 3*10-14s
und Start der Simulation kann man sehr gut die Vermischung der beiden
Gase beobachten.

typisches Spurbild für die kin. Gastheorie: Knicke in der Bahn weisen auf Zusammenstöße hin.
3) Beispiel zur Chaos-Theorie: chaos1.mds, chaos2.mds
Zielsetzung: Es soll die wohl bekannteste Aussage der Chaos-Theorie
verdeutlicht werden; kleinste Ursachen können fatale Folgen haben.
Diese Aussage ist für die Simulation physikalischer Vorgänge
(z.B. Erforschung der Klimaveränderung, Hurricane-Erforschung) von
großer Wichtigkeit.
Das in diesem Zusammenhang häufig zitierte Schmetterlingsbeispiel
(Der Flügelschlag eines Schmetterlings kann einen Orkan in einem anderen
Teil der Erde hervorrufen.) scheint für viele eine extreme Übertreibung
darzustellen. Und wenn dies für einen Normalbürger auch nicht
mit negativen Konsequenzen verbunden ist, so kann eine Vernachlässigung
der "Tatsache Chaos" im Bereich der Industrie zu millionenschweren
Verlusten führen, denn bereits simpelste algebraische Terme, wie die
des quadratischen Potentials verhalten
sich nach wenigen Iterationsschritten hochgradig chaotisch. Werden diese
Effekte bei der Gestaltung und Auswertung eines industriellen Simulationsprogrammes
nicht berücksichtigt, können Fehlkonstruktionen die Folge sein,
die unter Umständen den Ruin für eine Firma bedeuten.
Aufbau: Der Deutlichkeit halber wurde eine einfache zweidimensionale
Anordnung gewählt. Als Potential ist das quadratische eingestellt.
Der Cutoff wurde auf 1m gesetzt, d.h. er ist abgeschaltet,
da dies länger als die Diagonale des Kastens (maximaler Teilchenabstand)
ist. Dadurch wird das Potential zwar physikalisch unsinnig, aber es ergeben
sich sehr starke Kraftwirkungen.
Die Ensembles der Dateien "chaos1.mds" und "chaos2.mds"
sind vollkommen identisch bis auf die z-Koordinate des rot markierten Teilchens.
In "chaos2.mds wurde sie an der 18.Stelle um 1 erhöht (Anmerkung:
MDS zeigt die Koordinaten nur auf 17 Stellen gerundet an).
Dies entspricht einer Abweichung von 0.0000000000000002 Prozent.
Durchführung und Beobachtungen: (Anmerkung für Lehrer:
Wird dieser Versuch vor der Klasse vorgeführt könnte man die
Schüler an dieser Stelle raten lassen, wie viele Rechenschritte es
dauern wird, bis sich der Fehler äußert.) Wird nun die Simulation
gestartet, so bleiben bei "chaos1.mds" die Teilchen in einer
Ebene, doch bei "chaos2.mds" dauert es nur 230 Schritte bis die
ersten Teilchen die Ebene verlassen.
Führt man den selben Versuch mit Lennard Jones Potential durch, so
dauert es 2200 Schritte, obwohl dieses Potential
r in einer viel höheren Potenz enthält. Dies ist leicht dadurch
erklärt, daß das quadratische Potential ohne Cutoff
sehr extreme Werte erzeugt, während die des Lennard Jones Potentials
in einem kleineren Intervall liegen, da es bei großen r im Gegensatz
zum quadratischen Potential gegen 0 und nicht gegen Unendlich geht. Man
sieht also, daß komplizierte Funktionen nicht zwangsläufig chaotischer
sind als einfache.


Ensemble nach 2500 Schritten (Lennard Jones): links ohne Fehler, rechts mit Fehler
Zielsetzung: Es sollen die Planetenbewegungen in einem "handlichen" Modell gezeigt und der Nachweis für die nicht auf Anhieb sichtbare Tatsache erbracht werden, daß die Keplerschen Gesetze vollständig im Gravitationsgesetz von Newton enthalten sind.
Aufbau: Der Aufbau besteht aus einem Zentralgestirn und zwei
darum kreisenden Planeten. Die Masse des Sterns entspricht der unserer
Sonne, die des roten Planeten unserer Erde und die Masse des magentafarbenen
Planeten der Venusmasse.
Da die Bahnen der Planeten in unserem Sonnensystem zu sehr kreisförmig
sind, wurden fiktive Ellipsenbahnen gewählt
(im Folgenden werden jedoch trotzdem die Namen Erde und Venus für
die Planeten benutzt). Das Verhältnis der Radien der beiden Planeten
entspricht der Realität, aus Darstellungsgründen wurde der Sonnenradius
jedoch kleiner gewählt.
Durchführung und Beobachtungen:
a) Das erste Kepler-Gesetz sagt aus, daß die Bahnen der Planeten
elliptisch sind, und die Sonne in einem der
Brennpunkte liegt.
Wenn man Display/Smiley windows/slime tracks
aktiviert und die Simulation eine Weile laufen läßt, so kann
man diese Aussage anschaulich bestätigen.
Um den mathematischen Nachweis führen zu können, muß man
zuerst die maximalen und minimalen x- und y-Werte der beiden Planetenbahnen
bestimmen. Die Hälfte der Differenz ymax-ymin
ergibt dann die Länge der kurzen Halbachse b
(bErde=1.03*1011m,
bVenus=5.65*1010m)
und aus den x-Werten folgt die Länge der langen Halbachse a
(aErde=1.10*1011m,
aVenus=6.35*1010m).
Aus dem kürzesten Abstand dk zur Sonne
errechnet sich die lineare Exzentrizität mit e=a-dk
(eErde=3.89*1010m,
eVenus=2.92*1010m).
Die Bedingung e2=a2-b2
ist beide Male sehr gut erfüllt (Abweichung von e jeweils kleiner
als 1%).
b) Dem zweiten Kepler-Gesetz zufolge überstreicht der Vektor von
der Sonne zum Planeten in gleichen Zeiten immer gleiche Flächen. Dies
soll exemplarisch an je zwei Flächen gezeigt werden. Hierzu denke
man sich eine vertikale Linie durch den Mittelpunkt der Sonne. Der Teil
der Ellipsenfläche links davon sei F1
und die Fläche rechts davon sei F2.
Aus den oben ermittelten Daten kann man F2=b/a*[a2*p/2-e*
sqrt(a2-e2)-a2*arcsin(e/a)]
und F1=abp-F2
berechnen (F2Erde=9.95*1021m2,
F2Venus=2.46*1021m2,
F1Erde=2.56*1022m2,
F2Venus=8.81*1021m2).
Um die Zeiten zu bestimmen, in denen der jeweilige Entfernungsvektor die
Flächen überstreicht, wird der Schrittzähler auf 0 gesetzt
(Experiment/reset step counter), sobald
der betrachtete Planet an der Grenze zwischen den beiden Flächen ist.
Dann wird die Simulation gestartet und angehalten, sobald der Planet die
entsprechende Fläche umrundet hat. Die Messung ergibt tF1Erde=72000Schritte
und tF2Erde=28000Schritte,
sowie tF1Venus=34000Schritte
und tF2Venus=9700Schritte.
Beide Male gilt tF1/tF2=F1/F2
mit hinreichender Genauigkeit.
c) Das dritte Kepler-Gesetz sagt aus, daß sich die dritten Potenzen
der langen Halbachsen zueinander so verhalten, wie die Quadrate der Umlaufzeiten.
Um die Umlaufzeiten zu bestimmen, wird der Schrittzähler auf 0 gesetzt,
und dann die Simulation laufen gelassen, bis der betrachtete Planet nach
10 Umläufen (der größeren Genauigkeit wegen) wieder am
Ausgangspunkt angekommen ist. So ergibt sich für die Umlaufzeit der
Erde (TErde=1.00*105Schr.)
und der Venus (TVenus=4.40*104Schr.).
Die Abweichung T2Erde/T2Venus
von a3Erde/a3Venus
ist geringer als 1%, womit das Gesetz als erfüllt angesehen werden
kann.
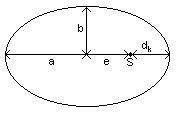 Die
Planetenbahnen sind Ellipsen mit der Sonne in einem Brennpunkt.
Die
Planetenbahnen sind Ellipsen mit der Sonne in einem Brennpunkt.
a große Halbachse
b kleine Halbachse
dk minimaler Abstand Planet - Sonne
e lineare Exzentrizität
S Sonne
Alle Rechte am Programm Molekular-Dynamik-Simulator, sowie an dieser Dokumentation gehören Matthias Benkmann.
Feedback bitte an Matthias Benkmann (m.s.b (a) gmx.net)